John Pople、Larry A. Curtiss、Krishnan Raghavachari、Paul C. Redfern らにより開発された非経験的分子軌道法に基づいた計算手法。分割して計算することにより計算コストを下げている。DFT の交換相関汎関数のパラメータの設定・フィッティングを行う際に参照するベンチマークとして用いられることもある計算手法の一つ。
目次
内容
最初の Gaussian-1 theory は 1989 年に発表された。それ以降、改良が加えられている。G1 は参考文献 1、G2 は参考文献 2,3,4、G3 は参考文献 5,6、G4 については参考文献 7 を参照。2004 年に John Pople がなくなってしまったので、参考文献 6 以降は Larry A. Curtiss、Krishnan Raghavachari、Paul C. Redfern により執筆されている。
Gaussian 公式ページ
Gaussian-1 Theory (G1)
G1 法の計算は次の流れで行われる。
- step1 構造最適化 HF/6-31G

- step2 さらに精密な構造最適化 MP2(FU)/6-31G
 //HF/6-31G
//HF/6-31G
- step3 MP4SDTQ(FC/6-31G
 //MP2(FU)/6-31G
//MP2(FU)/6-31G
- step4 diffuse 関数部分の抽出
![Rendered by QuickLaTeX.com \[{\Delta}E(+) = E(MP4/6-311+G^{**})-E(MP4/6-311G^{**})\]](http://computational-chemistry.com/top/wp-content/ql-cache/quicklatex.com-56a70a5a90fe742b862c0ccd9eb82449_l3.png)
- step5 polarization 関数の 2
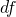 部分の抽出
部分の抽出
![Rendered by QuickLaTeX.com \[{\Delta}E(2df) = E[MP4/6-311G^{**}(2df)]-E(MP4/6-311G^{**})\]](http://computational-chemistry.com/top/wp-content/ql-cache/quicklatex.com-c95ac03cf8f642437dc4633654066bd7_l3.png)
- step6 配置間相互作用の修正 QCISD(T)/6-311G
 (post-MP4 として用いられている。)
(post-MP4 として用いられている。)
![Rendered by QuickLaTeX.com \[{\Delta}E(QCI) = E[QCISD(T)/6-311G^{**}]-E(MP4/6-311G^{**})\]](http://computational-chemistry.com/top/wp-content/ql-cache/quicklatex.com-f91f055342c387cbd845b9a0f2a204ab_l3.png)
- ここで、これまでの修正を足す
![Rendered by QuickLaTeX.com \[E(combined) = E(MP4/6-311G^{**})+{\Delta}(+)+{\Delta}E(2df)+{\Delta}E(QCI)\]](http://computational-chemistry.com/top/wp-content/ql-cache/quicklatex.com-36084c8c39155f4407b644422e6bea8d_l3.png)
これは、QCISD(T)/6-311+G
 (2df) の近似的な計算結果を示しているが、上述のように 4 分割して計算することにより計算コストが大幅に小さくなっている。
(2df) の近似的な計算結果を示しているが、上述のように 4 分割して計算することにより計算コストが大幅に小さくなっている。 - step7 ここで、基底関数に起因する誤差をさらに修正する(“higher level correction” = HLC)。
![Rendered by QuickLaTeX.com \[\DeltaE(HLC) = -0.19n_{\alpha}-5.95n_{\beta}\]](http://computational-chemistry.com/top/wp-content/ql-cache/quicklatex.com-c18a2874e5a350a6b049b27830188d3d_l3.png)
-
![Rendered by QuickLaTeX.com \[E_e = E_{combined}+{\Delta}E(HLC)\]](http://computational-chemistry.com/top/wp-content/ql-cache/quicklatex.com-5869532b68dd085d14ee9f022d277801_l3.png)
- step8 振動数計算と零点エネルギー
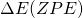 の計算
の計算
しかし、高い計算レベルで振動計算を行うのは難しいので、HF/6-31G* で振動計算し 0.8929 をかけたものを足す。
Gaussian で実行するには
実際に Gaussian で実行するには、キーワードセクションに G1 と入力するだけです。以下、input ファイルの例です。
%chk=Computational-chemistry-G1-sample.chk %mem=10000MB %nprocshared=16 #p G1 geom=connectivity Title Card Required 0 1 C -1.66195900 -0.63341800 0.33702100 H -1.50482000 -0.57004700 1.43330200 C -0.27428000 -0.78891900 -0.32543300 C -2.39264700 0.66131500 -0.00643800 H -0.05686900 -1.86455800 -0.32717100 H -0.34637300 -0.49907000 -1.38002900 C 0.88157000 -0.05169500 0.36152800 O -3.59040900 0.74824200 -0.17407900 H 0.68951700 1.02600200 0.35987500 H 0.92444400 -0.35712200 1.41767700 (以下略)
計算結果の log ファイルをテキストエディターなどで開き、”#p” で検索すると以下のように複数 step の計算が行われていることがわかります。
---------------------------
#p G1 geom=connectivity
---------------------------
中略
---------------------------------------------------------
#P Geom=AllCheck Guess=TCheck SCRF=Check HF/6-31G(d) Freq
---------------------------------------------------------
中略
--------------------------------------------------------------------
#P Geom=AllCheck Guess=TCheck SCRF=Check MP2(Full)/6-31G(d) Opt=RCFC
--------------------------------------------------------------------
中略
-----------------------------------------------------------------
#P Geom=AllCheck Guess=TCheck SCRF=Check QCISD(T,E4T)/6-311G(d,p)
-----------------------------------------------------------------
中略
---------------------------------------------------------
#P Geom=AllCheck Guess=TCheck SCRF=Check MP4/6-311+G(d,p)
---------------------------------------------------------
中略
----------------------------------------------------------
#P Geom=AllCheck Guess=TCheck SCRF=Check MP4/6-311G(2df,p)
----------------------------------------------------------
中略
Diagonal vibrational polarizability:
0.0000000 0.0000000 0.0000000
Temperature= 298.150000 Pressure= 1.000000
E(ZPE)= 0.042658 E(Thermal)= 0.045529
E(QCISD(T))= -40.405888 E(Empiric)= -0.024560
DE(Plus)= -0.000303 DE(2DF)= -0.019637
G1(0 K)= -40.407731 G1 Energy= -40.404859
G1 Enthalpy= -40.403915 G1 Free Energy= -40.425030
中略
Normal termination of Gaussian
Gaussian-2 Theory (G2)
G1 に対して次の 3 点の改良を行った(参考文献 2)。
- correction for nonadditivity of diffuse-sp and 2df basis set extensions
- a basis set extension containing a third d function on nonhydrogen atoms and a second p function on hydrogen atoms
- a modification of the higher level correction
汎関数のフィッティング
B3LYP などのハイブリッド型汎関数では、その混合率を決める際に G2 ベンチマークの物性値と合うように調整されている。
Gaussian-3 Theory (G3)
Gaussian-4 Theory (G4)
参考文献
- “Gaussian‐1 theory: A general procedure for prediction of molecular energies” John A. Pople, Martin Head‐Gordon, Douglas J. Fox, Krishnan Raghavachari and Larry A. Curtiss J. Chem. Phys. 1989, 90, 5622. DOI: 10.1063/1.456415
- “Gaussian‐2 theory for molecular energies of first‐ and second‐row compounds” L. A. Curtiss, K. Raghavachari, G. W. Trucks, and J. A. Pople, J. Chem. Phys. 1991, 94, 7221. DOI: 10.1063/1.460205
- “Assessment of Gaussian-2 and density functional theories for the computation of enthalpies of formation” L. A. Curtiss, K. Raghavachari, P. C. Redfern, and J. A. Pople, J. Chem. Phys. 1997, 106, 1063. 10.1063/1.473182
- “Assessment of Gaussian-2 and density functional theories for the computation of ionization potentials and electron affinities” L. A. Curtiss, K. Raghavachari, P. C. Redfern, and J. A. Pople, J. Chem. Phys. 1998, 109, 42. DOI: 10.1063/1.476538
- “Assessment of Gaussian-3 and density functional theories for a larger experimental test set” L. A. Curtiss, K. Raghavachari, P. C. Redfern, and J. A. Pople, J. Chem. Phys. 2000, 112, 7374-7383. DOI: 10.1063/1.481336
- “Assessment of Gaussian-3 and density-functional theories on the G3/05 test set of experimental energies” L. A. Curtiss,P. C. Redfern, and K. Raghavachari J. Chem. Phys. 2005, 123, 124107. DOI: 10.1063/1.2039080
- “Gaussian-4 theory” L. A. Curtiss,P. C. Redfern, and K. Raghavachari J. Chem. Phys. 2007, 126, 084108. DOI: 10.1063/1.2436888
関連する記事
汎関数一覧に戻る
計算手法に戻る