様々なベンチマーク論文で良い傾向を示している B97 と ![]() B97 系 汎関数の成り立ちについて本記事では解説しております。gaussian ではB97-1, B97-2, B97-D,
B97 系 汎関数の成り立ちについて本記事では解説しております。gaussian ではB97-1, B97-2, B97-D, ![]() B97,
B97, ![]() B97X,
B97X, ![]() B97X-D の 6 種類が使用可能です。関連文献も下の方にまとめてありますので、論文で引用する際にはご活用ください。
B97X-D の 6 種類が使用可能です。関連文献も下の方にまとめてありますので、論文で引用する際にはご活用ください。
概要
B97 系汎関数の基になっている B97 汎関数は、その名前からも分かる通り アクセル・ベッケ Axel D. Becke によって 1997 年に報告されました(参考文献 1, 2)。一番最初に報告された半経験的汎関数であり、全部で 13 個の半経験的パラメーターを使っています。この汎関数はハートリーフォック交換積分を一定割合混合しているため混成汎関数でもあります。
![]()
その後、93 と 147 の系の 2 つのテストセットを用いてパラメーターをフィッティングし直し、半経験的パラメーターを 15 用いている HCTH が Nicholas C. Handy らにより報告されました(参考文献 3 )。HCTH はハートリーフォック交換積分を混合しないので GGA 汎関数です。B97 系汎関数はこの汎関数を補正あるいは改良した汎関数です。さらにパラメーターを改良した B97-1 も報告されました(参考文献 4)。
そして、現在様々なベンチマークで良い結果を残している ![]() B97 汎関数は、2008 年に UC Berkley の Martin Head-Gordon らのグループによって報告されました。長距離補正を含んでいることが主な改良点です。また、同じ論文にて short-range HFX を加えた
B97 汎関数は、2008 年に UC Berkley の Martin Head-Gordon らのグループによって報告されました。長距離補正を含んでいることが主な改良点です。また、同じ論文にて short-range HFX を加えた ![]() B97X 汎関数も報告されています(参考文献 7 )。また、同じく 2008 年に Martin Head-Gordon らにより報告された
B97X 汎関数も報告されています(参考文献 7 )。また、同じく 2008 年に Martin Head-Gordon らにより報告された ![]() B97X-D 汎関数は Grimme の半経験的分散力補正を加えたものです(参考文献 8 )。
B97X-D 汎関数は Grimme の半経験的分散力補正を加えたものです(参考文献 8 )。
本サイトでこれまで紹介した文献でも ![]() B97系 を使用した計算がいくつかあります。ベンチマーク論文などを見ていると比較的良好な結果を与えている気がします。
B97系 を使用した計算がいくつかあります。ベンチマーク論文などを見ていると比較的良好な結果を与えている気がします。
参考:Rh/Ru を用いた σ-bond activation に適した汎関数!
参考:NHC-Pd 触媒を用いた溝呂木・ヘック反応に最適な汎関数!
参考:リン酸化反応の QM/MM
参考:プロパギルアミンと二酸化炭素を基質とした銀触媒による 5/6 員環形成反応の選択性に関する計算
gaussian での使い方
gaussian09 E.01 と gaussian16 A.03 のソースコードファイル utilnz.F の中をみると、以下の 6 つの B97 系汎関数が実装されていることがわかります。
- B97-1
- B97-2
- B97-D
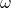 B97
B97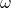 B97X
B97X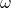 B97X-D
B97X-D
論文では、 B97-3、B97-K など他にも B97 系の汎関数はありますが、gaussian に実装されているのは上記の 6 つだけです。
ちなみに、IOp 番号は、以下のようになっています
- IOp(3/74=-20) : B97-1
- IOp(3/74=-21) : B97-2
- IOp(3/74=-42) : B97-D
IOp(3/74=-59) : B97-D (DFT-D3) - IOp(3/74=-56) :
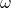 B97
B97 - IOp(3/74=-57) :
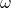 B97X
B97X - IOp(3/74=-58) :
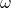 B97X-D
B97X-D
input ファイルで オメガ ![]() をどのように入力するのか疑問に思う方もいるかもしれませんが、ダブリュー w で代用します。wB97 や wB97XD のように入力すれば認識されます。
をどのように入力するのか疑問に思う方もいるかもしれませんが、ダブリュー w で代用します。wB97 や wB97XD のように入力すれば認識されます。
(例) %mem=4GB %nprocshared=4 #p opt wB97XD/6-31+G(d,p)
様々な汎関数の成り立ちや特徴などについて詳しく知りたい方は、密度汎関数の基礎(KS物理専門書)を読まれてはいかがでしょうか?
記事中に間違い等ある場合は、コメント欄、twitter またはメールにてお知らせいただけると幸いです。
参考文献
- B97 (“Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals” A.D. Becke, J. Chem. Phys. 1997, 107, 8554. DOI: 10.1063/1.475007)
- B97 (“A new inhomogeneity parameter in density-functional theory” A.D. Becke, J. Chem. Phys. 1998, 109, 2092. DOI: 10.1063/1.476722)
- HCTC (“Development and assessment of new exchange-correlation functionals” Fred A. Hamprecht, Aron J. Cohen, David J. Tozer & Nicholas C. Handy J. Chem. Phys. 1998, 109, 6264. DOI: 10.1063/1.477267
- B97-1 (“Assessment of exchange correlation functionals” Aron J. Cohen and Nicholas C. Handy, Chem. Phys. Lett. 2000, 316, 160–166. DOI: 10.1016/S0009-2614(99)01273-7)
- B97-2 (“Hybrid exchange-correlation functional determined from thermochemical data and ab initio potentials” Philip J. Wilson, Thomas J. Bradley, and David J. Tozer, J. Chem. Phys. 2001, 115, 9233-9242. DOI: 10.1063/1.1412605)
- B97-D (“Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction” Stefan Grimme, J. Comput. Chem. 2006, 27, 1787-1799. DOI: 10.1002/jcc.20495)
- wB97 & wB97X (“Systematic optimization of long-range corrected hybrid density functionals” J.-D. Chai and M. Head-Gordon, J. Chem. Phys. 2008, 128, 084106. DOI: 10.1063/1.2834918)
- wB97X-D (“Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections” J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys. 2008, 10, 6615-6620. DOI: 10.1039/b810189b)
- “Long-Range Corrected Hybrid Density Functionals with Improved Dispersion Corrections”
Y.-S. Lin, G.-D. Li, S.-P. Mao, J.-D. Chai, J. Chem. Theory Comput., 2013, 9, 263–272. DOI: 10.1021/ct300715s
関連する記事
- DFT は、正確な関数を目指す道から外れつつある
- アクセル・ベッケ Axel D. Becke
- Rh/Ru を用いた σ-bond activation に適した汎関数!
- NHC-Pd 触媒を用いた溝呂木・ヘック反応に最適な汎関数!
- リン酸化反応の QM/MM
- プロパギルアミンと二酸化炭素を基質とした銀触媒による 5/6 員環形成反応の選択性に関する計算
- HCTH
- Nicholas C. Handy
- B3LYP
- mPW1PW91
- M06 / M06-2X
- Minnesota 汎関数はどれくらい正確なのか?
- PBE0 混成汎関数
- 汎関数の選び方