密度汎関数法(density functional theory : DFT)は、種々の物質群の特性計算に幅広く応用されている電子状態理論であり、分子軌道法と双璧をなす第一原理計算手法です。
分子軌道法が、シュレーディンガー方程式を近似的に解いて波動関数を直接求めるのに対し、DFT法は、電子密度を試行関数に用いて変分原理を適用することによりは導関数を経由すること無く物性計算を行ないます。電子数に比例して次元が増大する波動関数に比べ、常に次元が一定な電子密度を試行関数に用いることにより計算コストは格段に低くなります。また、近年では、その精度は分子軌道法と同等のものにまでなりました。
DFT計算の精度は、交換相関汎関数の精度及び応用範囲で決定されます。完璧な交換相関汎関数を求める方法はなく、現在使われているものは、原子分子の正確な計算結果や実験データに基づいて調整されたパラメータを含むものが多いです。
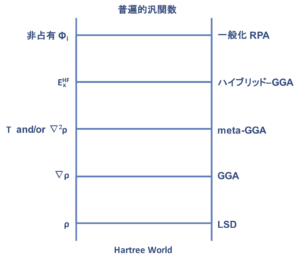
交換相関汎関数は、その近似の仕方により以下のように分類できます。
混成GGA(hybrid-GGA)
: GGAをHartree-Fock交換を使って補正。
- B3LYP 混成汎関数
- PBE0 混成汎関数
- HSE 混成汎関数
- mPW1PW91 汎関数
半経験的汎関数
局所密度近似(LDA)
: 電子密度ρのみで表現される。
一般化勾配近似(GGA)
: LDAを密度勾配∇ρを使って補正。
LDA・GGA 交換汎関数
- B88 交換汎関数
- PW91 交換汎関数
- PBE 交換汎関数
- revPBE 交換汎関数
- 無変数(parameter-free)交換汎関数
LDA・GGA 相関汎関数
- VWN-LDA 相関汎関数
- PW-LDA 相関汎関数
- PW91 相関汎関数
- PBE 相関汎関数
メタGGA(meta-GGA)
: GGAを二次密度勾配∇2ρや運動エネルギー密度 τ を使って補正。
- VS98 メタ交換・相関汎関数
- PKZB メタ交換・相関汎関数
- TPSS メタ交換・相関汎関数
- FT98 メタ相関汎関数
- KCIS メタ相関汎関数
ダブルハイブリッド汎関数
プログレッシブGGA(progressive-GGA)
: 併用する汎関数により形を変える
汎関数の開発は現在進行形で行われており、普遍的汎関数に徐々に近づいていると考えられている。ジョン・パデュー John Perdew はその様子を 2005 年の論文で Jacob’s ladder(ヤコビの梯子) として表現している(参考文献 1)。
gaussian で使うことのできる汎関数
gaussian 16 では、以下の汎関数が使えます。
mPW1PW91 B1LYP LG1LYP mPW1LYP mPW1PBE mPW3PBE PBE1PBE PBE3PBE BA1PBE BA3PBE B1B95 B98 HCTH93 B971 B972 HCTH147 HCTH407 O3LYP OHSE2PBE PBEh1PBE OmPW1PW91 OmPW1LYP OmPW1PBE OmPW3PBE tHCTH tHCTHhyb X3LYP BMK TPSSh OHSE1PBE M05 M052X OAPF CAM-B3LYP LC-wPBE B97D APF APFD PAPF PAPFD B2PLYP mPW2PLYP B2PLYPD mPW2PLYPD HSEH1PBE M06HF M06L M06 M062X wB97 wB97X wB97XD B97D3 B2PLYPD3 HISSbPBE HISSaPBE SOGGA11 M11 SOGGA11X M11L N12 MN12L N12SX MN12SX LC-wHPBE MN15L MN15 M08HX PW6B95 PW6B95D3 DSDPBEP86 PBE0DH PBEQIDH
gaussian09 E.01 では以下の汎関数が使用可能です。
VWN5 Lee, Yang and Parr Perdew 81 Perdew 81 + Perdew 86 VWN VWN + Perdew 86 Odom-Scuseria #1 PW91 PBE VSC Bc95 B98 HCTH B97-1 B97-2 HCTH147 HCTH407 VWN5+P86 LYP+VWN5 for scaling KCIS Becke-Roussel '88 PKZB TPSSc t-HCTH t-HCTH hybrid BMK M05 M05-2X OAPF B97-D APF PAPF M06-HF M06-L M06 M06-2X wB97 wB97X wB97X-D revTPSSc SOGGA11 M11 SOGGA11-X M11-L N12 MN12-L N12-SX MN12-SX
参考文献
“Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits”
John P. Perdew, Adrienn Ruzsinszky, Jianmin Tao, Viktor N. Staroverov, Gustavo E. Scuseria & Gábor I. Csonka J. Chem. Phys. 2005, 123, 062201. DOI: 10.1063/1.1904565