スピン状態依存的な光環化反応の計算

ブログ, 一般的な話題

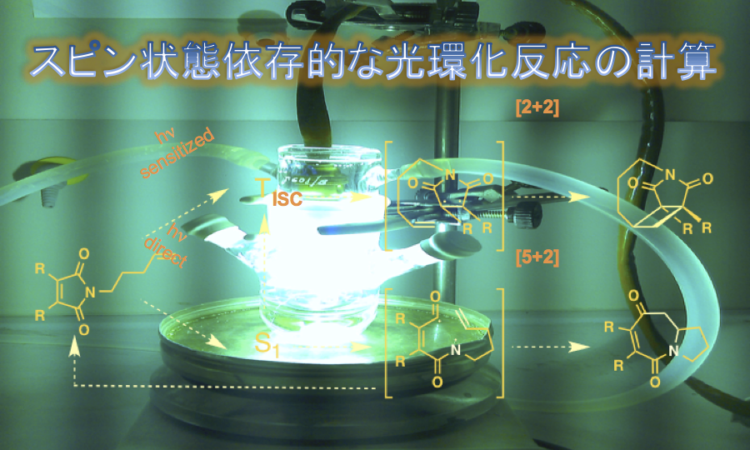
スピン状態依存的に異なる反応性を示す光環化反応について計算化学を用いた解析が行われました。JCC に論文が出ていましたので、簡単に紹介します。

“Theoretical Studies of Spin State-Specific [2 + 2] and [5 + 2] Photocycloaddition Reactions of N-(1-penten-5- yl) maleimide”
Xiang-Yang Liu, Pin Xiao, Wei-Hai Fang, and Ganglong Cui, J. Comput. Chem. 2017, in press, DOI: 10.1002/jcc.24897

目次

  1. 概要
  2. 計算レベル
  3. 感想
  4. 参考文献
  5. 関連する記事
  6. 汎関数一覧に戻る
  7. 計算手法に戻る

概要

N-alkenyl maleimide は、[2 + 2] および [5 + 2] 光環化付加に対してスピン状態に特異的な化学選択性を示すことが見出されている。しかし、反応メカニズムは依然として不明である。この研究では、高レベルの計算手法（DFT、CASSCF、およびCASPT2）を用いて、S_1 状態および T_1 状態の N-alkenyl maleimide の [2 + 2] および [5 + 2] 光環化付加反応経路を探索した。S_1 状態では [5-2] 光環化付加反応には活性化障壁がなく、圧倒的に支配的であることが分かった。[2 + 2] 光環化付加反応はその大きな障壁のために、S_1 状態では重要ではない。反対に、T_1 状態では [2 + 2] 光環化付加反応は、[5 + 2] 光環化付加反応よりもずっと有利である。反応機構としては、S_1 [5 + 2] および T_1 [2 + 2] 光環化付加反応の両方をもに stepwise に進行する。S_1 [5 + 2] 光環化付加反応において、ethenyl 部分の二級炭素が最初に maleimide 部分の窒素原子と反応し、S_1 中間体を形成する。その後、内部転換により S_0 状態になる。 T_1 [2 + 2] 光環化付加反応では、ethenyl 部分の末端炭素原子は最初にmaleimide の炭素原子を攻撃し、続いて交換交叉( T_1 –> S_0 ) により S_0 状態の中間体を与える。今回の計算結果は実験結果を合理化するだけでなく、反応機構に関して新たな知見を与えた。

計算レベル

中間体の構造最適化に関しては、T_1 と S_0 のは UB3LYP-D が用いられ、S_0 と S_1 の遷移状態の構造最適化には CASSCF (10 electrons in 8 orbitals) が、T_1 の遷移状態構造最適化には UB3LYP-D3 が用いられました。また、一点計算にはCASPT2 が用いられました。PCM で アセトニトリルの溶媒効果が見積もられています。

基底関数は 6-31G* が用いられています。UB3LYP-D を用いた計算には gaussian09 が、CASSCF と CASPT2 の計算には MOLCAS8.0 が用いられました。

感想

もともとの反応が報告された論文は参考文献 1。

個人的に、スピン状態が変化する反応やラジカル反応の計算に非常に興味を持っていますし、Crossing-point optimizations ってどのようにするんだろうって疑問でした。
今回は、”Penalty-function-based two-state crossing-point optimization” という方法を用いたようです。数式的には以下のように表されるようです。詳しくは、参考文献2-4。

f(R) = \frac{E_I+E_J}{2} + c_1c_2^2\rm{ln}[1 + {(\frac{E_J-E_I}{c_2})^2]

個人的に知る限りでは、Cross-point の計算は非常に時間がかかると聞いたことがあるのですが、この方法ではどの程度の計算コストなのか気になるところです。

S_0 状態では、もっとも低い遷移状態でも 37 kcal/mol 程度のエネルギーが必要であり、光励起なしでは反応が進行しないことがわかります。
実験結果と計算結果がきちんと相関しており、これほどきれいに結果が出るもんなんだと驚きました。

参考文献

  1. “Reaction Control in Synthetic Organic Photochemistry: Switching between [5+2] and [2+2] Modes of Cycloaddition”
    C. Roscini, K. Cubbage, M. Berry, A. Orr-Ewing, K. Booker-Milburn,
    Angew. Chem. Int. Ed. 2009, 48, 8716-8720. DOI: 10.1002/anie.200904059
  2. “The Photoisomerization Mechanism of Azobenzene: A Semiclassical Simulation of Nonadiabatic Dynamics” C. Ciminelli, G. Granucci, M. Persico, Chem. Eur. J. 2004, 10, 2327-2341. DOI: 10.1002/chem.200305415
  3. “DL-FIND: An Open-Source Geometry Optimizer for Atomistic Simulations”
    J. Kastner, J. Carr, T. Keal, W. Thiel, A. Wander, P. Sherwood, J. Phys.
    Chem. A 2009, 113, 11856-11865. DOI: 10.1021/jp9028968
  4. “ChemShell—a modular software package for QM/MM simulations”
    S. Metz, J. K€astner, A. A. Sokol, T. W. Keal, P. Sherwood, WIREs Comput. Mol. Sci., 2014, 4, 101-110. DOI: 10.1002/wcms.1163

関連する記事

汎関数一覧に戻る

計算手法に戻る

コメントを残す（投稿者名のみ必須）