DFT 計算の進歩について

ブログ, 一般的な話題

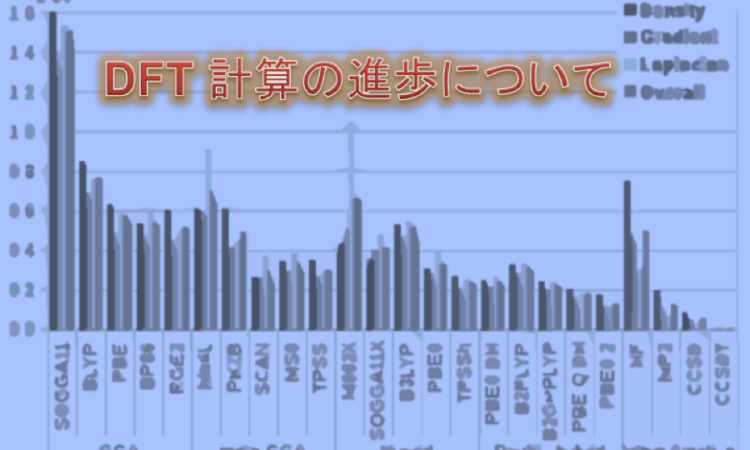
今年の初めに Science 誌にジョン・パデュー John Perdew らの”密度汎関数理論は、正確な関数を目指す道から外れつつある“という論文が掲載されました。

参考: DFT は、正確な関数を目指す道から外れつつある

論文中でドナルド・トゥルーラーDonald G. Truhlarらが開発した Minnesota 汎関数がフルボッコにされていたことも記憶に新しいと思います。そして、その数日後に反論の論文が arXiv に公開されたことも、みなさん憶えていらっしゃると思います。

参考：いやいや、密度汎関数理論は正確な関数を目指す道から外れてはいない！

これで一件落着か、、、と思っていたら、最近、また DFT 計算の進歩に関する論文が発表されました！

“Electron Density Errors and Density-Driven Exchange-Correlation Energy Errors in Approximate Density Functional Calculations”
Pal D. Mezei, Gabor I. Csonka, Mihaly Kallay
J. Chem. Theory Comput. in press. DOI: 10.1021/acs.jctc.7b00550

目次

  1. 概要
  2. 計算レベル
  3. 内容
  4. 関連する記事

概要

その正式な導入以来、密度汎関数法は、分子化学や個体化学の分野で大きな成功を収めてきました。その中心原理によれば、多電子系の基底状態は電子密度で完全に記述することができるそうです。長い間、密度汎関数の研究ではエネルギー値のより正確な記述には、電子密度の正確な記述や近似方法の向上が必要であると考えられてきました。
最近の分析（Medvedev et al. Science 2017, 355, 49-52.）で、2,4または10個の電子を有する 14 個の原子（Be-Ne）およびカチオンに対して、近年普及しているが物理的にはあまり正しくない汎関数を用いると大きな誤差を与えるということが指摘されました。
密度汎関数法では、正確なエネルギーにもかかわらず、計算された電子密度に大きな誤差を与える可能性があります。この研究では、はるかに広範な結論が導き出されているが、著者が使用した方法論には改善が必要な場合があります。最も重要なのは、ベンチマークセットが圧縮された高電子密度の小さなカチオン原子に偏っていることです。今回の論文では、化学的に関連する電子密度を有する分子テストセットを構築し、未検討の二重ハイブリッドを含むいくつかの密度汎関数近似の性能が分析されました。
電子密度、その勾配、およびラプラシアンについて集中的な誤差測度を適用し、電子密度の誤差が semilocal exchange-correlation energy にどのように伝播するかが調べられました。 Medvedev et al. の広範な結論の確認が試みられましたが、異なるデータの解析方法を用いたため、細部が異なる結論にたどり着いたようです。最後に、電子密度の観点からグローバルハイブリッド法またはダブルハイブリッド法の背後にある理論的根拠を求めて、PBEベースのグローバルハイブリッドおよびダブルハイブリッド汎関数における exact exchange および second-order perturbative correlation の混合の役割も分析されています。

計算レベル

すべての計算は MRCC という量子化学計算ソフトを使って行われました。

不確かさを避けるために、可能な限り無限に近い grid が計算に使用されました。420-point Log3 radial grid（または水素原子用の 415-point Log3 grid） と 1202-point の角度 Lebedev grid。
基底関数系には、aug-cc-pVXZ および aug-cc-pwCVXZ（X = D、T、Q、5）基底系が用いられました。 Medvedevらの原子密度テストセット（B^{3+}、C^{4+}、N^{5+}、O^{6+}、F^{7+}、Ne^{8+}、Be、B^+、C^{2+}、N^{3+}、O^{4+}、F^{5+}、Ne^{6+}、Ne）に対して、 2電子系の場合は CCSD/aug-cc-pwCV5Z、それ以外の場合は CCSDTQ/aug-cc-pwCV5Z が用いられています。

今回の論文で用意された新たなテストセット (H_2, LiH, Li_2, LiF, BH_3, H_2O, HF, CO, N_2, F_2)に対しては、H_2 に対しては CCSD/aug-cc-pV5Z を用い、それより大きなものに対しては CCSDTQ/aug-cc-pwCV5Z が用いられました。

座標は、NIST Computational Chemistry Comparison and Benchmark Database から取ってきたようです。

用いられた汎関数は、SOGGA11, BLYP, PBE, BP86, RGE2, M06L, PKZB, SCAN, MS0, TPSS, M06-2X, SOGGA11X, B3LYP, PBE0, TPSSh, PBE0-DH, B2LYP, B2GPPLYP, PBE-QIDH, PBE0-2。
その他用いられた計算理論は、HF, MP2, CCSD, CCSDT です。

内容

以前の記事で紹介した Medvedev の論文では、正確なエネルギーを与える汎関数は電子密度も正確に計算することができると考えられてきたが、実際には違ったというのが大筋でした。今回の論文では、Medvedev らの論文で用いられた原子はあまり化学的に重要なテストセットではないということで、低分子のテストセットを用いて新たにベンチマークの測定が行われています。解析方法も変更されています。その結果、異なる結論が導き出されております。

例えば、meta-GGA レベルの TPSS 汎関数は、グローバルハイブリッド PBE0 汎関数よりもはるかに良い電子密度を算出できますし、半経験的に構築された M06L 汎関数は、LDA よりも明らかに優れた電子密度を与えることが示されています。 著者らはまた、特定のグローバルダブルハイブリッド法でより良い密度が得られることを示しています。 例えば、PBE0-2 ダブルハイブリッド汎関数は MP2 法の精度に近い精度で原子密度を算出しましたし、分子密度で MP2 の精度を上回りました。

今回の論文では、DFT と半局所交換相関エネルギーを density-driven error に関して比較することも行われました。Density-driven 交換相関エネルギー誤差は、これまでに報告されたのと同じ順序に必ずしも従うとは限らないことがわかりました。

半局所交換相関エネルギーでの density error と density-driven error の両方を考慮すると、精度の高い順に最も優れている汎関数は、PBE、TPSS または SCAN、TPSSh、および PBE0-2 であり、すべてが非経験的な起源を持つ汎関数でした。

これを見る限り Minnesota 汎関数はまたダメということなのでしょうか？ちなみに、管理人の身近ではMinnesota 汎関数はあまり評判がよくありません。。。

あと、PBE0DHってめちゃくちゃ時間かかるので、個人的はあまり使いたくないと思っています。

記事中に間違い等ある場合は、コメント欄、twitter またはメールにてお知らせいただけると幸いです。

関連する記事

コメントを残す（投稿者名のみ必須）