今年の初めに Science 誌に掲載されたジョン・パデュー John Perdew らの論文 “Density functional theory is straying from the path toward the exact functional” が非常に興味深い内容でしたので紹介したいと思います。日本語タイトルは「密度汎関数理論は、正確な関数を目指す道から外れつつある」。
“Density functional theory is straying from the path toward the exact functional”
Michael G. Medvedev, Ivan S. Bushmarinov, Jianwei Sun, John P. Perdew, Konstantin A. Lyssenko, Science 2017, 355, 49-52. DOI: 10.1126/science.aah5975
初期の頃の LDA 法が使われておりましたが、その後、LDA を凌ぐ GGA 法が登場しました。とりわけアクセル・ベッケ Axel D. Beckeが開発したハイブリッド汎関数(hGGA) B3LYP は素晴らしいものでしたし、meta-GGA の開発も盛んに行われました。エネルギーの値が正確になっていく一方で、最近開発された汎関数は電子密度が正確ではないものも増えてきました。中には、LDA 法よりも不正確なものもあります。
今回紹介する論文では、128 個の汎関数を選び CCSD-Full との誤差を調べ、年代別、種類別に分けて傾向をわかりやすい表にしています(実際の Figure は論文を見てください。)。
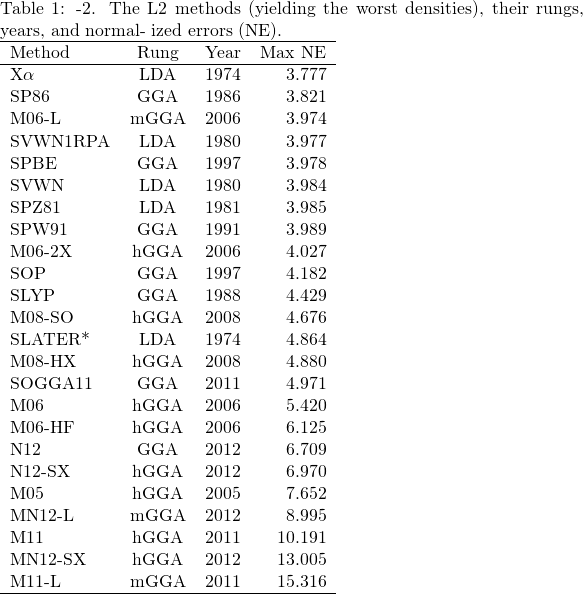
反応開発など低分子有機化学反応の計算においてポスト B3LYP の呼び声も高かった Minnesota 汎関数でしたが、今回の論文で調べられれた汎関数の中では最も誤差が大きかったです(下記 Table2)。
今回の比較から、
- 半経験的パラメータを含まない汎関数は、半経験的パラメータを含む汎関数に比べて、より正確な電子密度を与える。
- 半経験的パラメータを含まない汎関数は、ヤコブの梯子 Jacob’s Ladder に従って、近似方法が複雑になっていくに従って電子密度が正確になっていく(LDA → GGA → meta-GGA → hybrids の順に良くなっていく)。
という傾向が明らかになりました。
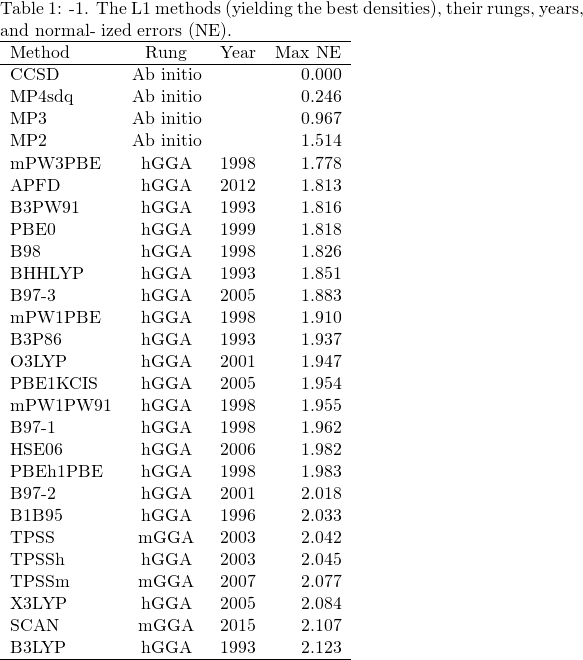
Table は、論文の値を参考に管理人が再構築しました。Table 1 は、最も良かった汎関数。Table 2 は、最も悪かった汎関数。
Table 1 は、post-HF 法と 20 個のハイブリッド汎関数と 3 個の meta-GGA から構成されています。成績の良かったハイブリッド汎関数は、参考文献 1 , 2 でアクセル・ベッケ Axel D. Becke が提案したように、3 つまたは 1 つのパラメータを含んでいました。また、PBE, mPW, B88 交換汎関数や PBE, mPW91, LYP 相関汎関数を含んでいるものが多かったです。
一方、Table 2 では 1985 年以前に発表された汎関数と最近のパラメータを多量に含む汎関数で構成されています。特に最近のパラメータを多量に含む汎関数は、エネルギーや geometry が正確性であるにも関わらず、電子密度の正確性が非常に低いという結果になっています。
著者らは、今後の汎関数の開発では長い間無視され続けてきた電子密度が重要な役割を担うであろうと述べています。より優れた汎関数の誕生には、新たな戦略が必要とされています。
管理人は、量子化学の専門家ではありません。もし記事中に誤りなどがございましたらコメント欄またはメールにてご連絡いただければ幸いです。
参考文献
- “Density-functional thermochemistry. III. The role of exact exchange” A. D. Becke, J. Chem. Phys. 98, 5648 (1993). DOI:10.1063/1.464913
- “Density‐functional thermochemistry. IV. A new dynamical correlation functional and implications for exact‐exchange mixing” A. D. Becke, J. Chem. Phys. 104, 1040–1046 (1996). DOI: 10.1063/1.470829
関連する記事