以前の記事で Threadripper での gaussian16 のベンチマークをお伝えしました。
その際、並列化効率が著しく悪いと述べましたが、その後検討を重ねたところ並列化効率が大幅に改善しました。
改善後は、
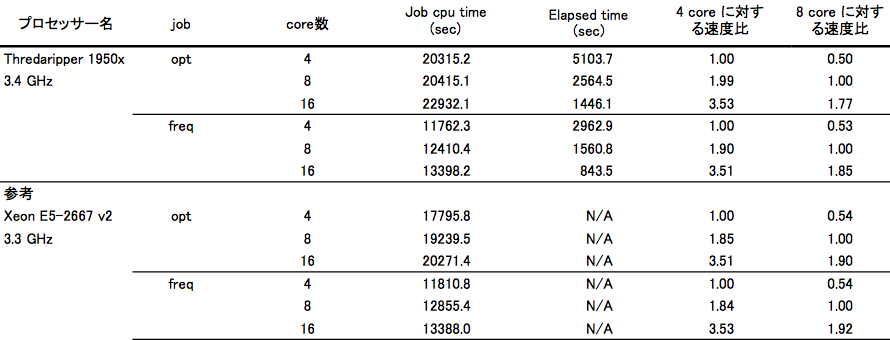
opt 計算で、4core –> 8core で計算速度 1.99 倍。8core –> 16core で 1.77 倍。4core –> 16 core で 3.53 倍。
freq 計算で、4core –> 8core で計算速度 1.90 倍。8core –> 16core で 1.85 倍。4core –> 16core で 3.51 倍でした。
以前の記事では、4core –> 16core で計算速度が 2 倍程度にしかならなかったのが、今回 3.5 倍になりましたので、大幅な改善と捉えることができます。
以下詳細を述べます。
英語版:Threadripper Parallel Efficiency improved ! Gaussian16 Benchmark
変更点
基本的なパソコンのセットアップは以前の記事を見てください。
前回はメモリが 2 枚挿し(16GB)でしたが、今回はメモリを 4 枚挿し(32GB)に変えたところ大幅に並列化効率が改善しました。また、NUMA mode と UMA mode についても今回検討を行いました。
計算方法
並列化効率については、前回と同様 vomilenine という天然物を用いて構造最適化と振動計算を行いました。
input ファイルは以下になります。お使いのブラウザ環境によっては、%CPU の前後に空行が挿入されてしまいますが、実際には空行はありません。
%mem=8GB %CPU=0-15 # opt B3LYP/6-31G(d) Title Card Required 0 1 C 2.77247700 -1.55726100 -0.24944000 C 2.57516800 -0.21391100 0.22236700 C 3.66258100 0.58993400 0.49571100 C 4.95487500 0.05924200 0.30006200 C 5.13835000 -1.24438700 -0.15742400 C 4.04078000 -2.07971400 -0.44110700 H 3.54022600 1.61215000 0.84659000 H 5.82063000 0.68647200 0.50832700 H 6.14732700 -1.63065000 -0.30202500 H 4.18101400 -3.09833800 -0.79798600 N 1.50857200 -2.23308200 -0.46688800 C 1.09205700 0.01376600 0.31548100 C 0.56508400 -1.38330300 -0.16916400 C 0.45169100 0.19038400 1.70181800 H 0.83716900 1.07864500 2.23417400 H 0.61400000 -0.67650100 2.36782500 C -1.02531100 0.35002700 1.28672300 H -1.62528500 0.84001900 2.08048000 C -0.92615500 -1.59776300 -0.23639300 H -1.16616400 -2.69064700 -0.25662300 N -1.59116700 -1.02041200 0.99900700 C 0.45662500 1.13244700 -0.55154600 H 0.50638000 0.83609200 -1.63113300 C -1.01485700 1.18415400 -0.05441000 H -1.34499800 2.22278200 0.13282400 C 1.18183100 2.47371100 -0.45244600 O 1.77040700 2.90633300 -1.41767100 C 1.12488300 3.24417800 0.83431200 H 1.96513800 3.95149200 0.90568700 H 0.20810900 3.84695700 0.89196200 H 1.14807000 2.59412400 1.72379300 C -1.43760100 -0.86406700 -1.51074000 H -2.21770900 -1.45377000 -2.02155200 H -0.63475100 -0.74431500 -2.26051300 C -1.99672600 0.50937600 -1.06002400 H -2.15238600 1.17083500 -1.93738400 C -3.07440500 -0.82309500 0.77399500 H -3.54334800 -0.53697600 1.74827200 O -3.70333500 -2.06174800 0.48837800 H -3.47163400 -2.39796600 -0.40177600 C -3.29369900 0.20245900 -0.33620000 C -4.47635800 0.74125600 -0.64594500 C -4.60024253 1.78394479 -1.77246740 H -4.05885576 2.66655486 -1.50265297 H -4.19662792 1.38069830 -2.67766766 H -5.63131953 2.02904648 -1.91979486 H -5.39456085 0.49863744 -0.15305581
並列化効率の改善
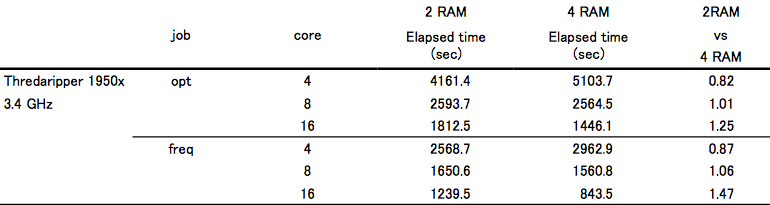
具体的な計算結果は以下になります。
並列化効率は、Xeon E5-2667 v2 と同様の値になりました。後ほど述べることとも関連するのですが、opt の速度は Xeon E5-2667 v2 よりも遅くなってしまいました。しかし、freq の速度は同じでした。
なぜ、こんな前世代の Xeon と比較するのかという声もあるかと思いますが、たまたま管理人が所有している計算機が Xeon E5-2667 v2 (8CPU64core) だからです。
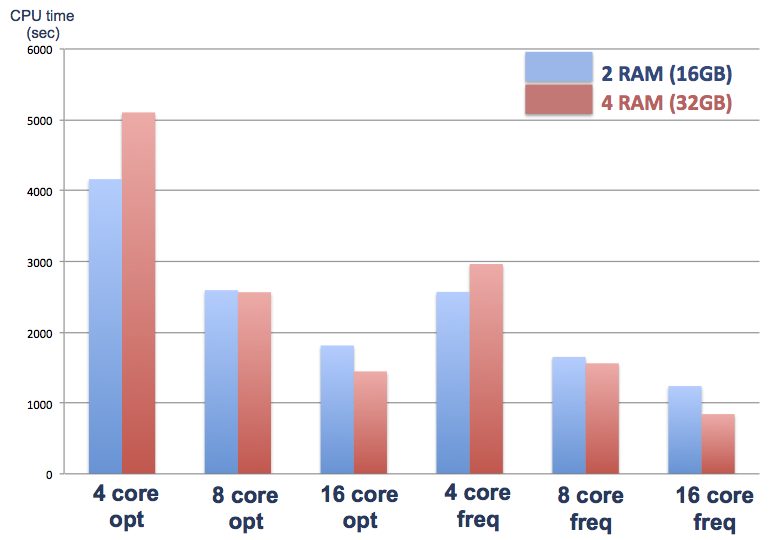
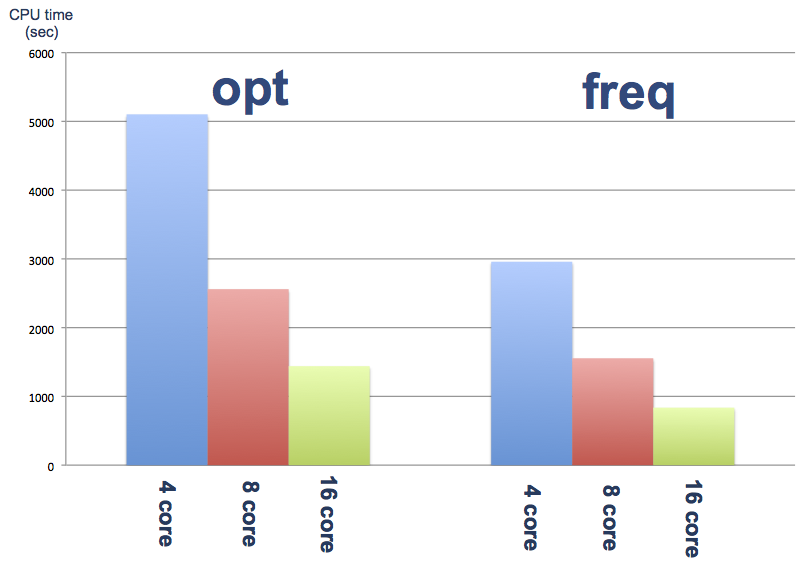
並列化効率をわかりやすく棒グラフにまとめました。
2枚挿し vs 4枚挿し
4 枚挿しに変更して、並列化効率は大幅に改善したのですが、4core 使用時の計算速度が約 15% 遅くなってしまいました。しかし、それだけが理由で並列化効率が上がったのではなく、16core 使用時の計算速度は opt で 25%、freq で 47% 高速化しています。
わかりやすく、棒グラフにしました。見てお分かりになるように、4core では 2枚挿しの方が早いですが、8core、16core では 4 枚挿しの方が早いです。
NUMA と UMA
メモリのモードの変更については、こちらのページを参考にしました。
MSI のマザーボードの BIOS 画面では、Advanced Setting の OC > DRAM Setting > Advanced DRAM Configuration > Misc Item > Memory interleaving から変更できます。
なお表記が
UMA mode(Distributed) = Die
NUMA mode(Local) = Channel
となっているため、若干わかりづらいです。
結論から言いますと、NUMA モードの方が計算速度は早いです。
freq で 約 5%、opt で約 2% NUMA の方が UMA よりも早いです。大きな分子を計算する場合には結構大きな差だと思います。
また MSI には Socket というメモリーモードもあったので試しましたが、UMA mode(Distributed, DIE) と全く同じ結果が得られました。
その他試したこと
コア数の指定ですが、%nprocshared ではなく、%CPU=0-15と指定した方が 約 2 % ほど速度が上がりました。
計算のために確保するメモリが多すぎると計算速度が低下するため、2枚挿しの時に 16 core を用いた計算でメモリの確保量を 16GB, 8GB, 4GB と変えましたが、ほぼ変化はなく、並列化効率にも改善は見られませんでした。
そもそも、メモリがおかしいと気づいたのは、test397 の計算で HF で計算していたのがきっかけです。HF など計算レベルが低いもの、または基底関数が小さいものの計算では並列化効率が高かったため、もしかしてメモリに問題があるかも?と思いました。
Gaussian はメモリ消費量が少ないので、システム全体で 16 GB で十分だろうと勝手に判断していたのが間違いでした。良い勉強になりました。
まとめ
4 枚挿しにして並列化効率は改善したものの、4coreでも計算速度は落ちたので、全体として計算効率が上がったのか微妙なところです。普段は 4core の job を 4 つ投げる場合が多いので。。。
Threadripper は最大 8 枚までメモリを認識するので、もしかしたらメモリを 8 枚挿しにしたらさらに 16 core の時の計算速度が上がるのでは?と思いましたが、どうなのでしょう。
しかし、メモリをあと 4 枚買う気にはなりません。。。
EPYC も基本的には Threadripper と同じため、EPYC を購入して多コアで計算するのも良いかもしれませんね。
気になっていた並列化効率も改善されたため、Threadripper はだいぶオススメです!
次回は、test397 と test310 についても計算を行いたいと思います。また、HF や MP2、基底関数のサイズを変えた場合についてもベンチマークをとっていきたいと思います。
参考文献
UMA と NUMA の違いが解説されています。
HP ProLiant DL980 G7でのGaussian09の評価
関連する記事
- Threadripper Gaussian16 ベンチマーク
- Threadripper 自作 PC 組み立て編【AMD】
- IRC 計算がうまくいかない時
- スピン状態依存的な光環化反応の計算
- Threadripper 正式発表【8月発売予定】
- 【Gaussian 16】デスクトップ PC で並列計算する際の注意点【Hyperthreading】
- スパコンランキング発表!日本はGREEN500上位独占!【2017年6月】
- 【AMD_Naples】正式名称はEPYCに決定!クロック数は2.8 GHz【基本スペックなど】
- GPU を用いた並列計算
- 自作 PC をつくってみた!
- Fedora25 に nVIDIA のドライバーをインストール
- 自作 PC を作ってみた!【OS 編】

TRはmcm のコアなので、だいたい8cのコアのcpu2個が一つのソケットに載っているようなものです。
8cごとにメモリチャンネルが2ある構造なので、メモリ4枚を使わないと全てのメモリチャンネルを使えないだけでなく、2枚では場合によっては一方のコアは他方のメモリコントローラを通してメモリにアクセスしなければならないので、性能が大きく下がります(メモリのレイテンシ及び帯域由来)。
4c8cのジョブをなげるのであれば、localで(できれば)使うコアを各mcm内で制限できれば理想的な計算速度を得られると思います。
もしできるのであれば、intelのデュアルソケットのシステムと比べると同様の傾向が得られるのではないでしょうか
コメントありがとうございます。大変勉強になりました。
intelのデュアルソケットのシステムは常にフル稼働で計算させておりますので、比較することはできませんが、今後新しく計算機を購入する際には注意したいと思います。
今後も、もし記事中に間違いなどありましたら、ご指摘いただけたら幸いです。