Coenzyme B12 依存性酵素 ONIOM 計算の汎関数ベンチマーク

ブログ, 一般的な話題

これまで当サイトで紹介してきたベンチマークは、ある一つの反応についてのベンチマークでした。しかし、実際の化学現象では複数の性質の異なる反応が連続して進行することもあり、単一の汎関数でそれぞれの反応すべてを同様の正確性で計算することは容易ではありません。

先日、J. Phys. Chem. A に Coenzyme B12 依存性酵素の ONIOM 計算での汎関数のベンチマークが報告されました。Coenzyme B12 が関わる酵素反応では、炭素-コバルト結合のホモリシスと水素移動反応が連続して、または協奏的に進行するため、両方の反応を正確に見積れる汎関数を見つけ出さなくてはならないという点に難しさがありました。今回紹介する論文では、16 個の汎関数でベンチマークを測定しています。

“Modeling the Reactions Catalyzed by Coenzyme B12 Dependent Enzymes: Accuracy and Cost-Quality Balance”
Christian R. Wick & David M. Smith
J. Phys. Chem. A in press. DOI: 10.1021/acs.jpca.7b11798

目次

  1. 概要
  2. 計算手法
  3. 結果
  4. 参考文献
  5. 関連する記事

概要


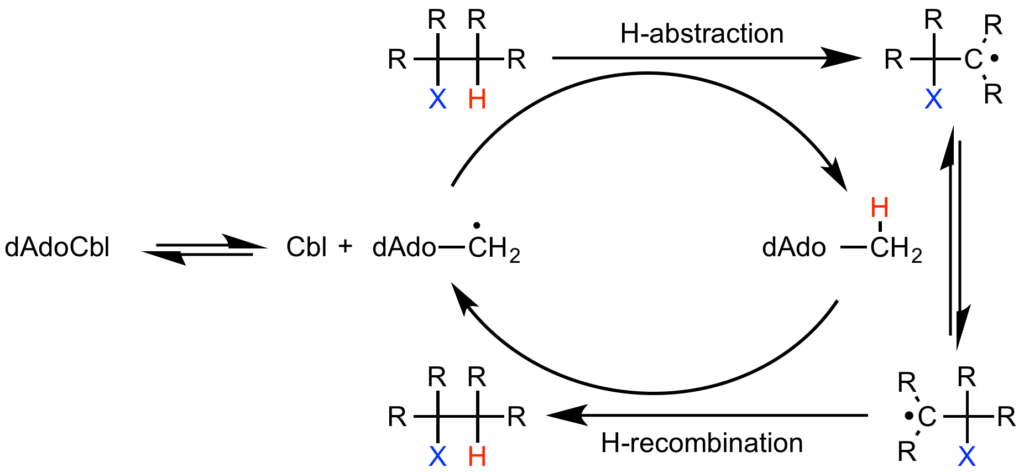
Coenzyme B12 依存性酵素によって触媒される反応では、炭素-コバルト結合のホモリシスにより反応が開始し、それに引き続く（または協奏的な）水素移動反応が起こります。したがって、この酵素反応を表すための計算モデルは、炭素-コバルト結合のホモリシスと水素移動反応の両方を正確に見積もる必要があります。計算系のサイズから DFT または QM/MM が適切な計算手法と考えられるが、この枠組み中のCo-Cホモリシスおよび水素移動反応の正確な記述は困難であり、様々な精度で議論の余地のある結果につながる可能性があります。本論文では 16 個の汎関数について検討を行ないました。水素引き抜き反応は、広範囲の補酵素 B12 反応に類似するように設計された 4 つの参照反応に基づいてモデル化されました。Co-C 開裂反応は、ONIOM（QM / MM）を用いて計算され、溶液相実験データと優れた一致を示した。また、系全体を DFT 計算した場合と同様の正確性が得らることがわかりました。本論文のベンチマーク測定により、meta-GGA の TPSS-D3 および M06L-D3 および meta hybrid M06-D3 が、両方のタイプの反応について 10 kJ/mol 未満の MUE で最良の総合性能を与えることを見出されました。本論文の成果は役にたつはずだから、みんな使ってね💕！

計算手法

すべての計算は gaussian09 を用いて行われました。
構造最適化は TPSS-D3/def2-SVP を用いて計算されました。ベンチマーク測定用の汎関数には、APFD, B3LYP-D3, BP86-D3, B97D, BLYP-D3, BMK-D3, M06, M06L, M06-D3, M062X-D3, MN12L, PBE-D3, PBE0-D3, TPSS-D3, ωB97XD が用いられ、基底関数には def2-TZVP が使われました。

QM/MM 計算の MM 部分には AMBER が使われています。

結果

論文中で使われている略語は、BDE は Co–C Bond Dissociation Enthalpy, MSE は Mean Signed Error, MUE は Mean Unsigned Error をそれぞれ表します。本記事中では省略しますが、単位はすべて kJ/mol です。

まず Co–C のホモリシスについて調べられました。
Coenzyme B12 は比較的大きな構造をしているので、簡略化した構造で計算をしたくなりますが、側鎖が有った方が実験値を良く再現するという報告があります（参考文献 1,2）。当たり前のことですが、大きな系で構造を省略する場合には、最初にきちんと調べておくのが良さそうですね。

まずは、Coenzyme B12 を Full DFT で計算しています。結果を見ますと汎関数によってだいぶバラツキがありました。例えば、B3LYP では Co–C 結合を過小評価しています。一方で、BP86-D3 は、実験値と比較的良い一致を示しています。また、TPSS-D3 が最も良い結果を与えているので、この結果を QM/MM の reference として用いることにしました。

ここでは結果を示しませんので、ONIOM 計算のベンチマークについては論文中の table 3 を参照してください。ここでは、実験値と比較されています。Co–C のホモリシス反応では 6 つの汎関数が良い結果を与えました。ハイブリッド汎関数の APFD、メタハイブリッド汎関数の M06-D3、2 つの meta-GGA M06L-D3 と TPSS-D3、2 つの GGA PBE-D3 と BLYP-D3。

参考：【Enthalpy】B3LYP での計算誤差について【Underestimation】

続いて、H abstraction についてベンチマーク誤差の測定が行われました。Reference としては、G3(MP2)-RAD が使われています。G3 については下の記事をご参照ください。

参考：Gaussian-X theory 、G-X ＿汎関数の評価方法

まずは、反応熱のついて比較が行われました。ここでは結果を示しませんので、論文中の table 4 を参照してください。この反応では、どの汎関数も MUE が 8 以下であり、比較的良い結果を与えています。中でも良い結果を示したのが M062X-D3 でした。MSE = 0.4, MUE = 1.6, LAD = 2.1 でした。もっとも悪い結果を示したのは M06L-D3 でした(MUE = 7.7)。この結果は、他の文献で報告されている傾向とも一致しているようです。

続いて、活性化エネルギーについて比較が行われました。ここでは結果を示しませんので、論文中の table 5 を参照してください。活性化エネルギーに関しても M062X-D3 がもっとも良い結果を示しました（MUE = 2.6）。また、Mo6L-D3 も比較的良い結果を与えました。一方で、BP86-D3 は MUE = 27.8 という非常に大きい誤差を与えています。

以上の Co–C のホモリシスと H abstraction の結果をまとめたものが以下の図になります。

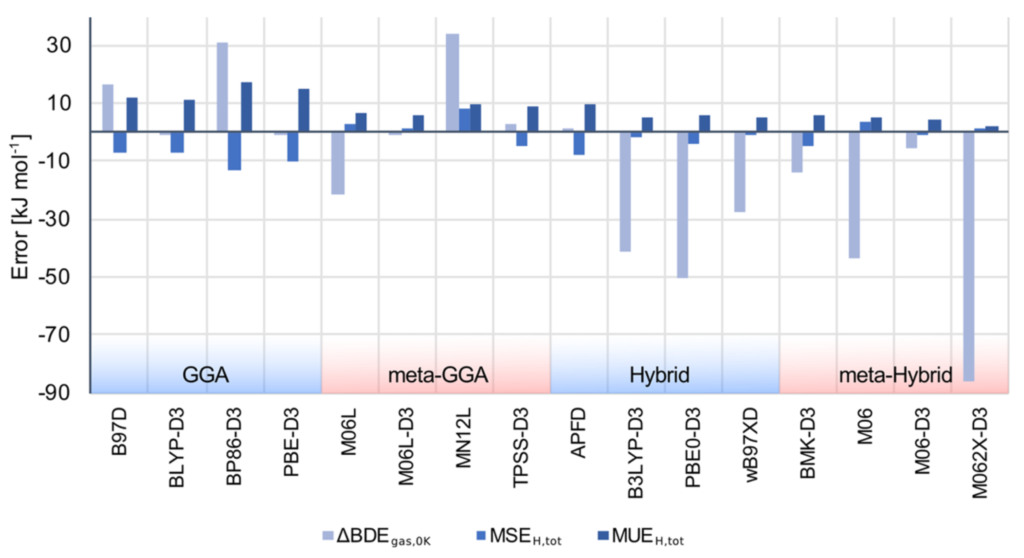
二つの反応で最適な汎関数はそれぞれ違います。そのため多少妥協する必要があります。これはドミノ反応などの多段階反応では仕方ないことと言えます。

全体の結果を総括すると、Local GGA 汎関数は水素引き抜き反応では最高のMUEを与え、今回用いた GGA 汎関数の半分が Co-C 開裂の正確な BDE を予測することができます。Meta-GGAは分散補正が含まれる限りは正確な BDE を与えることができ、水素引き抜き反応では MUE は 10 未満です。しかし、これは 水素引き抜き反応の正確性としては中程度です。それにも関わらず、Co-C 開裂の BDE の実験誤差が約 ±8 kJ/mol であることを考慮すると、Meta-GGAは確実に有望であると考えられます。 APFD および M06-D3 を除くハイブリッド汎関数は、Co-C ホモリシスの実験値を再現することができません。

明確な傾向がないためまとめることは難しいですが、結論としては M06-D3、M06L-D3、TPSS-D3 ならびに APFD の 4 つの汎関数がが両方の反応で良好な結果を与えています。さらに、計算コストのことも考慮すると、M06L-D3とTPSS-D3が最良の選択と言えそうです。

参考：revM06-L が発表されました。
参考：M06 / M06-2X
参考：Minnesota 汎関数はどれくらい正確なのか？

記事中に間違い等ある場合は、コメント欄、twitter またはメールにてお知らせいただけると幸いです。

参考文献

  1. “Co−C Bond Dissociation Energies in Cobalamin Derivatives and Dispersion Effects: Anomaly or Just Challenging?”
    Qu, Z., Hansen, A., Grimme, S. J. Chem. Theory Comput. 2015, 11, 1037−1045. DOI: 10.1021/acs.jctc.5b00007
  2. “Co−C Dissociation of Adenosylcobalamin (Coenzyme B12): Role of Dispersion, Induction Effects, Solvent Polarity, and Relativistic and Thermal Corrections.”
    Kepp, K. P. J. Phys. Chem. A 2014, 118, 7104−7117. DOI: 10.1021/jp503607k

関連する記事

コメントを残す（投稿者名のみ必須）