先日の記事：【Enthalpy】B3LYP での計算誤差について【Underestimation】 ではオレフィン環化反応の計算に最適な汎関数について紹介しました。今回の記事では Rh または Ru を用いた
-bond (C–H, O–H, H=H) activation の計算に関しての汎関数のベンチマークの論文を紹介したいと思います。
“Comparative Assessment of DFT Performances in Ru- and Rh- Promoted σ‐Bond Activations”
Yuanyuan Sun, Lianrui Hu, and Hui Chen, J. Chem. Theory Comput. 2015, 11, 1428−1438.
DOI: 10.1021/ct5009119
検討方法
今回の論文では 19 個の汎関数を用いて検討を行っています。CCSD(T)-F12 で計算した値と比較を行い、平均誤差を算出しています。検討に用いた汎関数は、GGA、 meta-GGA,、ハイブリッド、ダブルハイブリッドと新しいMinnesota 汎関数を用いています（ B3LLYP, PBE0, BMK, BP86, CAM-B3LYP, M06-L, M06, M06-2X, TPSS, TPSSh, 
B97X, B2GP-PLYP, B2-PLYP, OLYP, LC-PBE, N12, N12SX, MN12L, MN12SX ）。
中間体・遷移状態の構造最適化の計算では、汎関数に B3LYP を用いています。基底関数は H,C,N,O,F/P,S,Cl には cc-pVTZ/ccpV(T+d)Z を Ru,Rh には cc-pVTZ-PP をそれぞれ用いています。相対論効果の見積もりについては ECP28MDF を使用しています。
まず、今回 reference として用いる CCSD(T)-F12/aug-cc-pVDZ (以下ADZ) で計算した値が適切かどうかを確かめるため、CCSD(T)-F12/CBSとの比較を行っています。ADZ で計算した活性化エネルギーの値は、CBS で計算した値と Rh と Ru の系でそれぞれ 0.16、0.36 kcal/mol しか誤差がありませんでした。reaction energy に関しても 1 kcal/mol 以下の誤差でした。したがって、ADZ の計算結果は reference として妥当であると言えます。
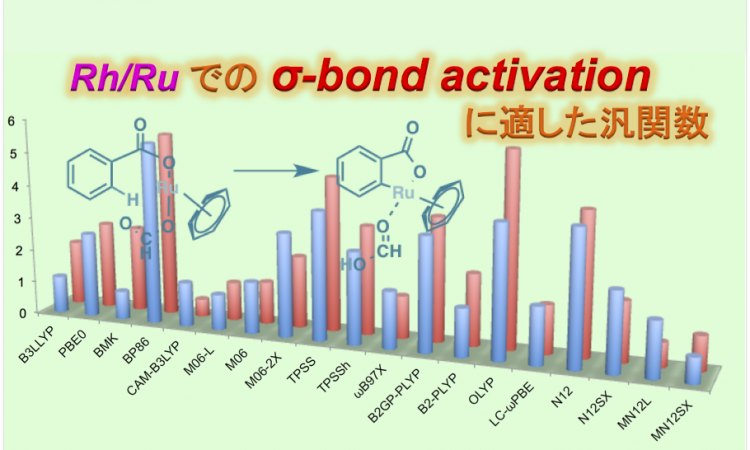
筆者らは、下図に示す反応の活性化エネルギー、reaction energy、分散力補正について計算を行いベンチマークを作成しました。
結果
- 活性化エネルギー
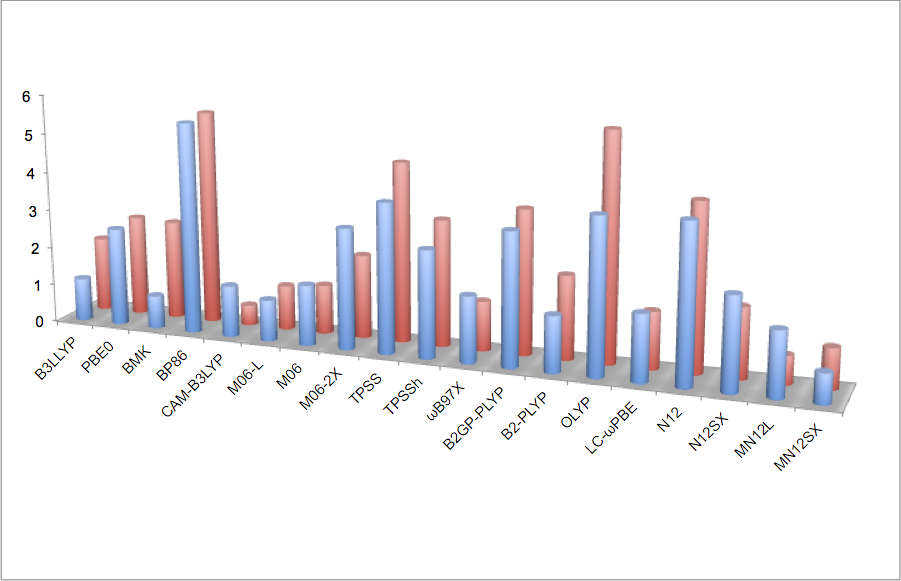
まず、活性化エネルギーについて調べたところ、もっとも最適な方法は MN12SX でした。また、Ru と Rh の計算結果を汎関数ごとに比べると、BMK と OLYP という例外を除けば、各々誤差が 1 kcal/mol であることがわかりました。つまり、Ru、Rh どちらの場合でも汎関数の挙動はほぼ一緒だということがわかりました。
誤差が 2 kcal/mol 以下の汎関数を小さい順に並べると MN12SX, CAM-B3LYP, M06-L, MN12L, M06, B97X, B3LYP, LC-PBE となりました。
- reaction energy
活性化エネルギーの場合とは異なり、reaction energy の計算では Ru, Rh の計算値が各汎関数ごとに誤差が大きくなるという結果が得られました。誤差が 2 kcal/mol 以下の汎関数を小さい順に並べると PBE0, CAM-B3LYP, N12SX の 3 つだけでした。
19 個の汎関数のうちもっとも悪かったのは BMK であり、5.28 kcal/mol の誤差がありました。BMK は活性化エネルギーの計算に最適化されているために、reaction enrgy の計算には不向きなのかもしれません。
- 分散力補正
最後に経験的分散力補正を行いベンチマークを取り直すと異なる結果が得られました。
活性化エネルギーの計算において誤差が 2 kcal/mol 以下の汎関数を小さい順に並べると 
B97X, B3LYP, CAM-B3LYP, M06-L,M06, B2-PLYP, LC-PBE となりました。B2-PLYP 以外は分散力補正を考慮する前でも良いパフォーマンスを示していました。
次に reaction energy の計算において誤差が 2 kcal/mol 以下の汎関数を小さい順に並べると PBE0, B3LYP, B97X, B2-PLYP となりました。分散力補正を入れない場合でも非常に良い結果を与えたことから、PBE0 は reaction energy の計算において非常に優秀と言えるかもしれません。
まとめ
分散力補正を考慮した計算で、活性化エネルギー、reaction energy ともに良い結果を示したのは B3LYP-D3, B97XD でした。Rh または Ru を用いた-bond (C–H, O–H, H=H) activation の計算には、この二つの汎関数を使うのが良いと思います。また、reaction energy の計算に限定するならば、 PBE0 が最適な汎関数です。
（注）この結果は、ADZ で計算した場合の結果になるので、もっと低い基底関数系で計算する場合には違った結果になると思います。
記事中に間違い等ある場合は、コメント欄、twitter またはメールにてお知らせいただけると幸いです。
参考文献
- “Comparative Assessment of DFT Performances in Ru- and Rh- Promoted σ‐Bond Activations”
Yuanyuan Sun, Lianrui Hu, and Hui Chen, J. Chem. Theory Comput. 2015, 11, 1428−1438.
DOI: 10.1021/ct5009119
関連する記事
- 【Enthalpy】B3LYP での計算誤差について【Underestimation】
- Diels-Alder 反応に最適な汎関数はどれ？
- B3LYP とは？
- mPW1PW91 とは？
- M06 / M06-2X とは？
- B88 交換汎関数 とは？
- Minnesota 汎関数はどれくらい正確なのか？
- PBE0 混成汎関数とは？
- GPU を用いた並列計算
- 構造最適化の閾値は、何を意味しているのか？
- 量子化学計算で a.u. を使う理由 〜Why Atomic Unit?〜
