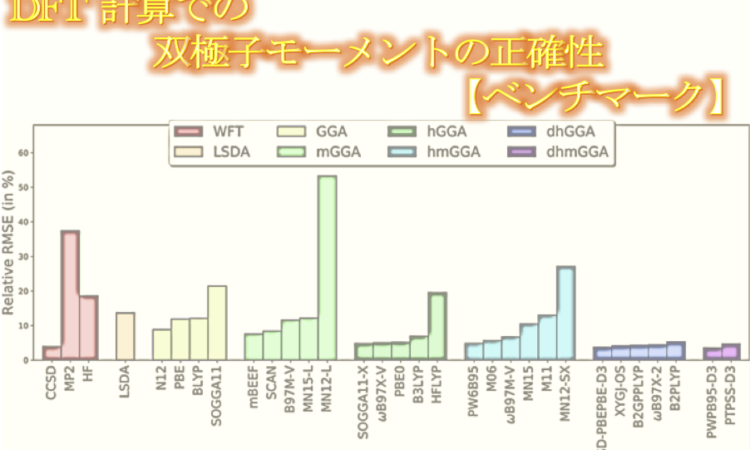
DFT 計算での双極子モーメントの正確性【ベンチマーク】

ブログ, 一般的な話題

DFT 計算での双極子モーメントの正確性に関するベンチマークが マーティン・ヘッドゴードン Martin Head-Gordon のグループから発表されました。

“How Accurate Is Density Functional Theory at Predicting Dipole Moments? An Assessment Using a New Database of 200 Benchmark Values”
Diptarka Hait & Martin Head-Gordon
J. Chem. Theory Comput. 2018, 14, 1969–1981. DOI: 10.1021/acs.jctc.7b01252

目次

  1. 概要
  2. 計算手法
  3. 結果
  4. 参考文献
  5. 関連する記事

概要

双極子モーメントは、極性分子の電子密度の正確性を測るためのシンプルで一般的な尺度です。双極子モーメントは、電場と同様に分子同士の相互作用に関係します。最近開発された密度汎関数の双極子モーメント計算の精度を評価するために、著者らは CCSD(T)/complete basis set limit で、基準となる 200 個の双極子モーメントのデータベースを作成しました。この新しいデータベースは、88 個のよく使われている最近開発された密度汎関数の性能を評価するために使用されました。結果として、ダブルハイブリッド汎関数が最良の性能を示しました（RMS: 約 3.6-4.5％ ）。これはCCSD での 4% RMS とあまり変わりません結果です。多くのハイブリッド汎関数も良好な結果を与え、RMS は 5-6％ の範囲でした。しかし、いくつかの汎関数では大きなエラーを示し、局所密度近似汎関数は全体的にハイブリッド汎関数やダブルハイブリッド汎関数よりも悪い結果でした。

計算手法

全ての計算は Q-Chem4 を用いて行われました（著者の Martin Head-Gordon は、Q-Chem の founder の一人です）。

分子の座標は NIST Computational Chemistry Database から取得されており、それぞれの汎関数での最適化はされていません。ただし、BH_2F と BH_2Cl の二つに関しては、MP2/cc-pVTZ で構造最適化されています。

構造最適化で MP2 を利用した理由には

as MP2 equilibrium geometries in general are known to be sufficiently accurate

と記述し、G3 の論文（参考文献 1） を引用しています。G3 については、以下の記事を参照してください。

参考：Gaussian-X theory 、G-X _汎関数の評価方法

また、非共有結合のある分子については、closed-shell のものは NCCE31 から open-shell のものは TA31 から座標を取得したようです。

supporting information には、全ての分子の座標と計算結果をまとめた Excel ファイルがあるため、結果を再現することができます。

結果

今回のベンチマークでは、計 152 分子がテストされました。まずは、これらの分子郡を二つのグループに分けました。81 個のスピン偏極の無いグループ (NSP: Non Spin-Polarized) と71 個のスピン偏極のあるグループ (SP: Spin-Polarization) です。

CCSD, MP2 または DFT では NSP 分子で極端に悪い結果を与えることはあまり無いですが、SP 分子の双極子モーメントの計算は NSP に比べれば、まだまだ challenging らしいです。

様々なベンチマーク論文で reference として用いられている CCSD(T) ですが、Coulson-Fischer point (参考文献 2) では精度が落ちるそうです。この論文では、以下のように書いてありました。

Indeed, the accuracy of CCSD(T) itself becomes questionable close to the Coulson-Fischer point of the FH PES due to the appearance of kinks. This led us to investigate CCSD(2) as an alternative benchmark in such situations, due to its renormalization of the one-body terms.

CCSD と CCSD(2) は Coulson-Fischer point でも理にかなった挙動を示していますが、CCSD(T) は少しおかしな曲線を描いています（論文中 Fig.1）。しかし、Coulson-Fischer point よりも短い距離や長い距離の場合には、いずれも同様の挙動を示しています。そのため、問題ないとしていくつかの分子には CCSD(T) が使われています。

全体として、DFT は \mu を正確に求めることができていました。とりわけダブルハイブリッド汎関数は CCSD と同程度の正確性でした。ハイブリッド汎関数も RMS 6% 以下で求めることができており、比較的正確です。計算コストを小さくしたい場合は、ハイブリッド汎関数を使うのが良いかもしれません。

今回テストした 22 個のハイブリッド汎関数のうち良い結果を与えたものは、PBE0 や B97-2 のように古いものでした。新しいもので良い結果を与えたのは、SOGGA11-X と \omegaB97X-V だけでした。また、hybrid mGGA は hybrid GGA に比べて特に改善は見られなかったため、汎関数がきちんと進歩しているかという点にに関して疑問です。

今回のベンチマーク測定の結果を受けて著者らは、”電子密度の計算に関しては、ダブルハイブリッド汎関数を除くと、ここ数年であまり進歩が見られていない” と述べています。もちろん今回最も良い結果を与えた GGA (N12) と mGGA (mBEEF) は最近のものであり、古い PBE や TPSS などに比べて良好な結果を与えていますが、その他の汎関数に関しては LSDA と同程度または劣る結果を与えています。

DFT の電子密度計算の正確性の問題に関しては、Perdew も以前に指摘していましたね。

参考：DFT は、正確な関数を目指す道から外れつつある

このようなベンチマーク測定は、自分の取り組んでいる反応系に最適な汎関数を見つける上でも重要ですが、汎関数が正しい方向に進化していることを確認する点でも有用ですね。

記事中に間違い等ある場合は、コメント欄、twitter またはメールにてお知らせいただけると幸いです。

参考文献

  1. “Gaussian-3 (G3) theory for molecules containing first and second-row atoms.”
    Curtiss, L. A.; Raghavachari, K.; Redfern, P. C.; Rassolov, V.; Pople, J. A.
    J. Chem. Phys. 1998, 109, 7764−7776. DOI: 10.1063/1.477422
  2. “I. XXXIV. Notes on the molecular orbital treatment of the hydrogen molecule.”
    Coulson, C. A.; Fischer,
    Philos. Mag. 1949, 40, 386−393. DOI: 10.1080/14786444908521726
  3. Coulson-Fischer theory

関連する記事

コメントを残す（投稿者名のみ必須）