あけましておめでとうございます。
昨年 11 月、12 月は、多忙のため記事の更新ができませんでしたが、今年はもっと更新していきたいと思います。
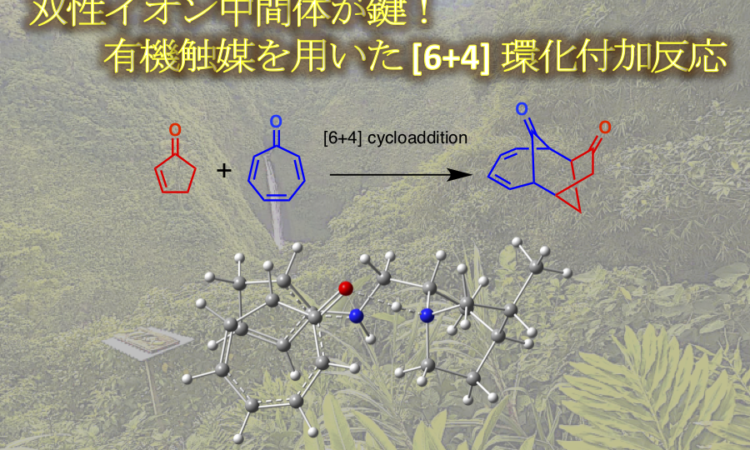
さて、もう 4 ヶ月も前になってしまいますが、シンコナアルカロイド有機触媒を用いた [6+4] 環化付加反応の計算化学の論文が Ken Houk のグループから出ましたので、簡単に紹介したいと思います。
“Organocatalytic [6+4] Cycloadditions via Zwitterionic Intermediates: Chemo‑, Regio‑, and Stereoselectivities”
Peiyuan Yu, Cyndi Qixin He, Adam Simon, Wei Li, Rasmus Mose, Mathias Kirk Thøgersen, Karl Anker Jørgensen & K. N. Houk
J. Am. Chem. Soc. 2018, 140, 13726-13735. DOI: 10.1021/jacs.8b07575
概要
2-cyclopentenone と tropone を基質とし、有機触媒を用いた [6 + 4] 付加環化反応の化学選択性および立体選択性のメカニズムおよび起源が、計算と実験を用いた複合的な研究によって明らかにされました。シンコナアルカロイド一級アミン触媒および酸添加剤の存在下で、2-cyclopentenone は cross-dienamine 中間体を形成した後、双性イオン中間体を経て段階的に [6 + 4] 付加環化反応が進行します。tropone の酸素原子とプロトン化された quinuclidine との間の強い水素結合相互作用を特徴とする律速段階の遷移状態は、高度に periselective な [6 + 4] 環化付加反応の方向性を決定します。この遷移状態における強力な水素結合相互作用の重要性は、酸添加剤の濃度が反応の収率およびエナンチオ選択性に対して影響を与えることからも裏付けされます。さらに、対応する [4 + 2] 付加環化反応は、はるかに高いエネルギー障壁を有することから、[6+4] の反応機構の方がより確からしいです。 また、[6 + 4] 環化付加のエナンチオ選択性は、ジアステレオマーの遷移状態での水素-水素間の反発に由来します。
計算手法
計算は全て gaussian09 で行われています。構造最適化は、B3LYP/6-31G(d) で、SMD で1,4-dioxane の溶媒効果を見積もられています。一点計算は、M06-2X/6-311+G(d,p) で行われています。
Thermal correction として B3LYP/6-31G(d) で計算した unscaled vibrational frequencies を M06-2X/6-311+G(d,p) の electronic energies に加え、free energy としています。(こういった補正をわざわざ Method に記述しくれるって、だいぶ親切だと思います。管理人も同様の補正を行なう場合があります。)
そして、この free energy を Truhlar の quasiharmonic correction で 100 cm![]() 以下の振動を 100 cm
以下の振動を 100 cm![]() に引き上げる補正をしています(参考文献)。
に引き上げる補正をしています(参考文献)。
Fig 2 の HOMO/LUMO の計算は、HF/6-31(d) で行われています。
内容
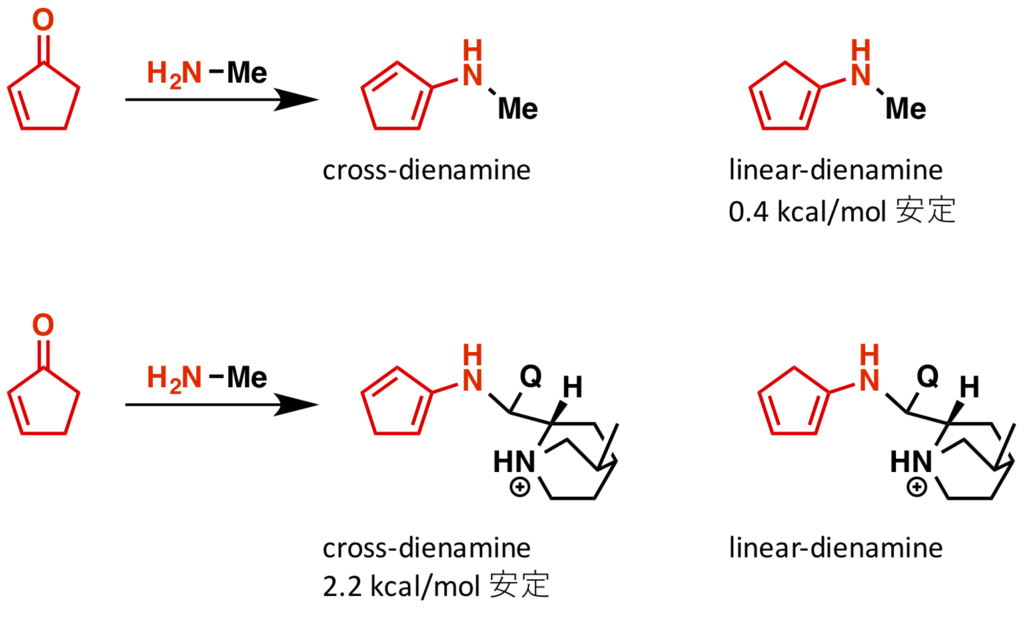
まずは、linear dienamine と cross-dienamine の比較が行われています(論文中 Fig 1)。通常は共役系が伸びるので linear dienamine の方が安定ですが、シンコナアルカロイドが付加すると cross-dienamine の方が安定になるそうです。
次に、[6+4] 付加環化反応のメカニズムが調べられています。協奏的ではなく、stepwize ということです。
参考:協奏的?それとも段階的? 〜concerted or stepwise?〜
上記の結果を踏まえて、cross-dienamine と tropone の付加環化反応の遷移状態が調べられています。全部で 6 種のコンフォメーションについて考察しています(論文中 Fig 3)。
その後論文中では、立体配座の解析や水素結合の重要性などが計算されています。また、カウンターイオンの影響を見積もるために、CSA や酢酸を置いて計算しています。 あまりここに描きすぎるのもまずいと思いますので、詳しくは論文をお読みください。
感想
ペリ環状反応の遷移状態を求める計算は意外と難しくはありません。しかし、高いレベルの雑誌に出そうとすると、しっかりと解析をしなくてはいけません。
複数の反応経路を計算し、ある経路の活性化エネルギーが他に比べて低いため優先するという計算だけで一応論文は書けてしまいます。しかし、ただエネルギーを比較するだけというのは、セミナーや学会などで発表していて非常に虚しくなってきますし、研究レベルは高くありません。
Ken Houk がなぜこんなに JACS を量産できるかと考えると、他の計算化学の論文とは異なり、有機化学の観点からしっかりと考察できているからだと思います。
今回の論文の Fig5 のようなエネルギーダイヤグラムや Fig 2 の HOMO/LUMO の図は、実験の片手間に行う計算でも簡単に作成することができます。しかし、ここで終わらずに、今回の論文の Fig 3, 4, 6, 7, 8, 9 のような考察ができると良い雑誌にアクセプトされるのではないかと思います。やっていることは、ゴーシュ配座の解析など非常に基本的なことですが、丁寧にここまでやることが重要なのでしょう。大多数の人は 6 個も TS を出して比較しないと思います。
単純なエネルギーの比較で終わらず、遷移状態”構造”についてより詳細に解析し、選択性の起源やメカニズムなどについて明らかにするレベルまで行きたいと管理人も常日頃自分自身に言い聞かせています。
管理人は、有機化学や計算化学を趣味とする一般人であり、専門家ではありません。そのため、記事中には誤りが散見されると思います。コメント欄、twitter またはメールなどで指摘していただけると非常にありがたいです。
参考文献
- Zhao, Y.; Truhlar, D. G. Phys. Chem. Chem. Phys. 2008, 10, 2813-2818. DOI: 10.1039/b717744e