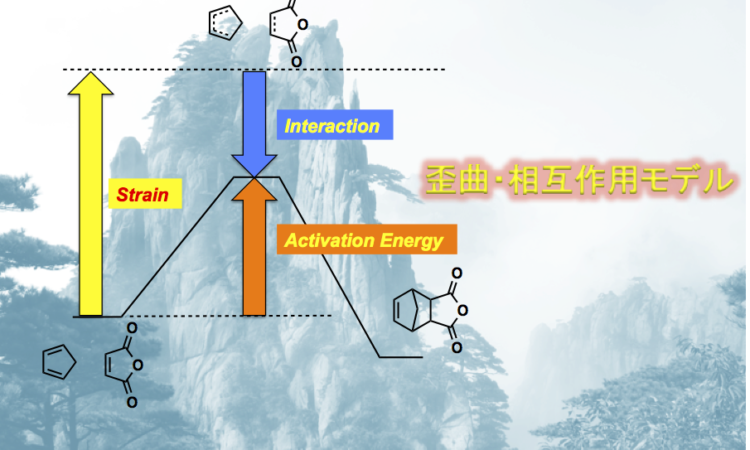
歪曲・相互作用モデル distorsion/interaction model

用語解説, 計算テクニック

ケンダール・ハウク Kendall N. Houk が提唱したモデル。同様のモデルが諸熊 Mrokuma、ビッケルハウプト Bickelhaupt らにより提唱されているが、それぞれ reactant deformation, activation-strain model という異なった名称で呼ばれている。

一番早く提唱したのは諸熊らだが、Houk, Bickelhaupt らが用いている distorsion/interaction model や activation-strain model という言葉の方が有名になりつつある。2017 年に Houk と Bickelhaupt が共著で Review を出したことや（参考文献 1 ）、Houk が自身の研究によく用いていることも関係していると思われる。

目次

  1. 内容
  2. 遷移状態構造の解析
  3. 実際にどう使うのか？
  4. 実用例
  5. 参考文献
  6. 関連する記事

内容

一言で簡単に説明すると、”原系から生成系へと至る過程でのエネルギー変化は、分子の構造の歪みによる不安定化と分子間の相互作用による安定化の和で表すことができる” という考え方です。反応座標を \xi とすると、このモデルでのエネルギーは次の式で表すことができます。

\Delta E(\xi) = \Delta E_{strain}(\xi) + \Delta E_{int}(\xi)

strain のエネルギーである \Delta E_{strain}(\xi) は、分子の剛直さによって決まります。\Delta E_{strain}(\xi) は多くの場合、正の値であり分子を不安定化させます。

一方、相互作用のエネルギーである \Delta E_{int}(\xi) は立体電子構造や反応する分子同士の方向性に依存します。\Delta E_{int}(\xi)　は多くの場合、負の値をとり分子を安定化させます。

しかし、以上述べたルールには例外も多く存在します。

遷移状態構造の解析

ポテンシャル曲面上でどこに遷移状態が存在するかは、\Delta E_{strain}(\xi)　と \Delta E_{int}(\xi) の関係によって決まります。すなわち、遷移状態では下式が成り立ちます。

\frac{d\Delta E_{strain}(\xi)}{d\xi} = -\frac{d\Delta E_{int}(\xi)}{d\xi}

activation-strain model の反応座標 (ASD: activation-strain diagram)を下に示します。横軸にその反応において重要な座標の変化を、縦軸にエネルギーを取ります。

相互作用の力は、次のように分解できます。

\Delta E_{int}(\xi) = \Delta V_{elst}(\xi) + \Delta E_{Pauli}(\xi) + \Delta E_{oi}(\xi) + \Delta E_{disp}(\xi)

\Delta V_{elst}(\xi) は準古典的な静電力、\Delta E_{Pauli}(\xi) は被占軌道間での反発、\Delta E_{oi}(\xi) は電子移動などの軌道間での相互作用、\Delta E_{disp}(\xi) は分散力です。

実際にどう使うのか？

activation-strain model は、基本的にはどの量子化学計算プログラムでも実行可能です。遷移状態から原系と生成系へといたる IRC 計算の各プロットにおいて、それぞれの基質に対して一点計算するだけです。（つまり、各プロットにおいて一点計算を二つすれば良いということ。）

しかし、\Delta E_{int}(\xi) を求めた後に、エネルギー分解して軌道相互作用の確認を行うには Amsterdam Density Functional (ADF) を使う必要があります。

実用例

S_N 2反応やペリ環状反応や遷移金属触媒を用いた C–C, C–H 結合活性化などの反応解析に用いられています。

ケンダール・ハウク Kendall N. Houk は、彼のライフワークともいうべき Diels Alder 反応で distorsion/interaction model を積極的に用いています。例えば、参考文献 2 では Cyclopentadiene, Cyclohexadiene, Cycloheptadiene の反応性の違いを遷移状態での歪曲具合でうまく説明しています。

記事中に間違い等ある場合は、コメント欄、twitter またはメールにてお知らせいただけると幸いです。

参考文献

  1. “Distortion/Interaction-Activation Strain Model to Analyze Reaction Rates” F. M. Bickelhaupt, Houk, K. N. Angew. Chemie. Int. Ed. 2017 in press DOI: 10.1002/anie.201701486
  2. “Theoretical Analysis of Reactivity Patterns in Diels−Alder Reactions of Cyclopentadiene, Cyclohexadiene, and Cycloheptadiene with Symmetrical and Unsymmetrical Dienophiles” Brian J. Levandowski and K. N. Houk, J. Org. Chem. 2015, 80, 3530−3537. DOI: 10.1021/acs.joc.5b00174
  3. Cheong, P. H.-Y.; Paton, R. S.; Bronner,S. M.; Im, G.-Y. J.; Garg, N. K.; Houk, K. N. J. Am. Chem. Soc. 2010, 132, 1267. DOI: 10.1021/ja9098643
  4. “Understanding reactivity with Kohn–Sham molecular orbital theory: 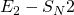E_2-S_N2 mechanistic spectrum and other concepts”
    F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114. DOI: 10.1002/(SICI)1096-987X(19990115)20:1<114::AID-JCC12>3.0.CO;2-L
  5. “Reactivity and Regioselectivity in 1,3-Dipolar Cycloadditions of Azides to Strained Alkynes and Alkenes: A Computational Study”
    Franziska Schoenebeck, Daniel H. Ess, Gavin O. Jones and K. N. Houk J. Am. Chem. Soc., 2009, 131, 8121–8133. DOI: 10.1021/ja9003624
  6. “Distortion/Interaction Energy Control of 1,3-Dipolar Cycloaddition Reactivity”
    D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646. DOI: 10.1021/ja0734086

関連する記事

コメントを残す（投稿者名のみ必須）